Understanding the Elo Rating System: The Grandfather of Competitive Rankings

I’ve always been fascinated by how we quantify the unquantifiable. How do you put a number on something as complex as chess skill? Or the quality of a product? Or even which taco joint in Atlanta deserves your hard-earned dollars?

Enter the Elo rating system - the OG of competitive rankings and the first algorithm I implemented in Elote.

The Origin Story: More Than Just Chess

The Elo rating system was developed by Hungarian-American physics professor and chess master Arpad Elo in the 1960s. The United States Chess Federation (USCF) adopted it in 1960, and FIDE (the International Chess Federation) followed suit in 1970.

What’s interesting is that Elo didn’t actually “invent” his system from scratch - he refined the existing Harkness rating system to make it more statistically sound. The guy was a professor of physics, after all, so he knew his way around a statistical distribution.

The beauty of Elo’s approach is that it wasn’t designed specifically for chess - it’s a general method for calculating the relative skill levels of players in zero-sum games. This generality is why we can now use it for everything from ranking NFL teams to sorting your product recommendations.

How Elo Works: The Simple Math Behind the Magic

At its core, the Elo system is beautifully simple. Here’s the basic idea:

1. Every player starts with a base rating (traditionally 1000 in chess)
2. When players compete, the winner takes points from the loser
3. The number of points exchanged depends on the expected outcome:
   • If a higher-rated player beats a lower-rated player (expected), few points change hands
   • If a lower-rated player beats a higher-rated player (upset), many points change hands

The mathematical formula looks like this:

New Rating = Old Rating + K × (Actual Score - Expected Score)

Where:

• K is a factor that determines how quickly ratings change (often 16, 24, or 32)
• Actual Score is 1 for a win, 0.5 for a draw, and 0 for a loss
• Expected Score is calculated using a logistic function based on the rating difference

The expected score formula is:

Expected Score = 1 / (1 + 10^((Opponent Rating - Player Rating) / 400))

This gives a probability between 0 and 1 representing the likelihood of winning.

Implementing Elo with Elote

Enough theory - let’s see how this works in practice with Elote. The implementation is dead simple:

from elote import EloCompetitor

# Create two competitors with initial ratings
magnus = EloCompetitor(initial_rating=2850)  # World champion level
amateur = EloCompetitor(initial_rating=1200)  # Casual player

# Check win probability
print(f"Amateur's chance of beating Magnus: {amateur.expected_score(magnus):.4%}")

# Let's say the amateur pulls off a miracle
amateur.beat(magnus)

# See how ratings changed
print(f"Magnus new rating: {magnus.rating}")
print(f"Amateur new rating: {amateur.rating}")

When you run this, you’ll see the amateur had a tiny chance of winning, but after the upset, their rating jumps significantly while Magnus loses a bunch of points.

You can also customize the K-factor to control how quickly ratings change:

# For a tournament with more stable ratings
tournament_player = EloCompetitor(initial_rating=1500, k_factor=16)

# For a new player whose rating is still being established
new_player = EloCompetitor(initial_rating=1500, k_factor=32)

Visualizing Elo: Win Probability and Rating Changes

Let’s visualize some key aspects of the Elo system:

import matplotlib.pyplot as plt
import numpy as np
import os

# Visualize win probability based on rating difference
rating_diffs = np.arange(-400, 401, 20)
win_probs = []

for diff in rating_diffs:
    player = EloCompetitor(initial_rating=1500)
    opponent = EloCompetitor(initial_rating=1500 + diff)
    win_probs.append(player.expected_score(opponent))

plt.figure(figsize=(10, 6))
plt.plot(rating_diffs, win_probs)
plt.axhline(y=0.5, color='r', linestyle='--', alpha=0.5)
plt.axvline(x=0, color='r', linestyle='--', alpha=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('Rating Difference (Player - Opponent)')
plt.ylabel('Win Probability')
plt.title('Elo Win Probability vs. Rating Difference')
plt.show()

# Visualize rating changes for different K-factors
rating_diffs = np.arange(-400, 401, 20)
k_factors = [16, 24, 32, 48]
rating_changes = {}

for k in k_factors:
    changes = []
    for diff in rating_diffs:
        player = EloCompetitor(initial_rating=1500, k_factor=k)
        opponent = EloCompetitor(initial_rating=1500 + diff)
        initial_rating = player.rating
        player.beat(opponent)
        changes.append(player.rating - initial_rating)
    rating_changes[k] = changes

plt.figure(figsize=(10, 6))
for k, changes in rating_changes.items():
    plt.plot(rating_diffs, changes, label=f'K={k}')

plt.axhline(y=0, color='r', linestyle='--', alpha=0.5)
plt.axvline(x=0, color='r', linestyle='--', alpha=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('Rating Difference (Opponent - Player)')
plt.ylabel('Rating Change After Win')
plt.title('Elo Rating Change vs. Rating Difference for Different K-factors')
plt.legend()
plt.show()

# Visualize rating changes for a fixed K-factor
plt.figure(figsize=(10, 6))
plt.plot(rating_diffs, rating_changes[32])
plt.axhline(y=0, color='r', linestyle='--', alpha=0.5)
plt.axvline(x=0, color='r', linestyle='--', alpha=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('Rating Difference (Opponent - Player)')
plt.ylabel('Rating Change After Win (K=32)')
plt.title('Elo Rating Change vs. Rating Difference')
plt.show()

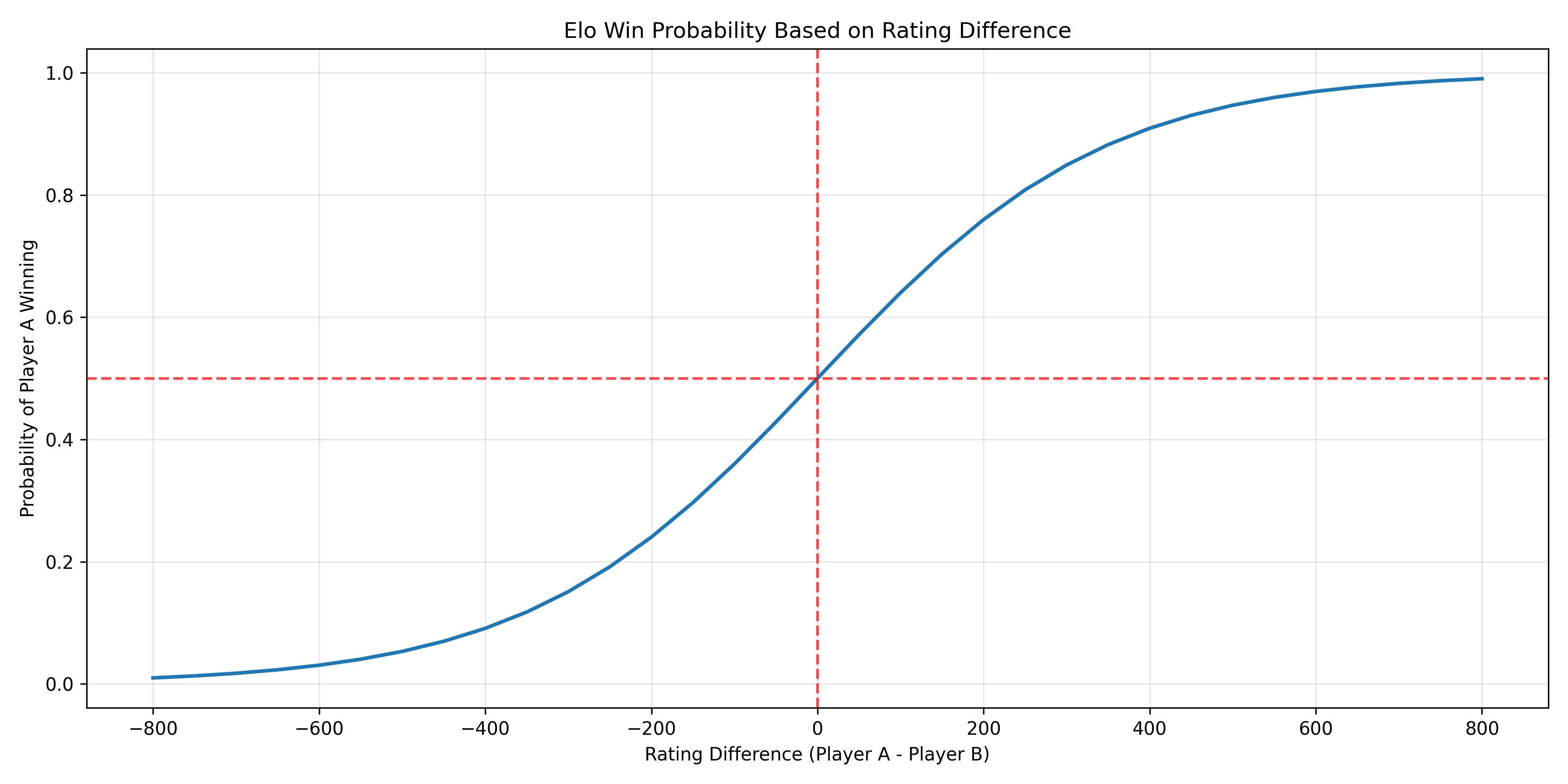
This chart shows how win probability changes with rating difference. A player with a 200-point advantage is expected to win about 75% of the time, while a 400-point advantage gives about a 90% chance of winning.

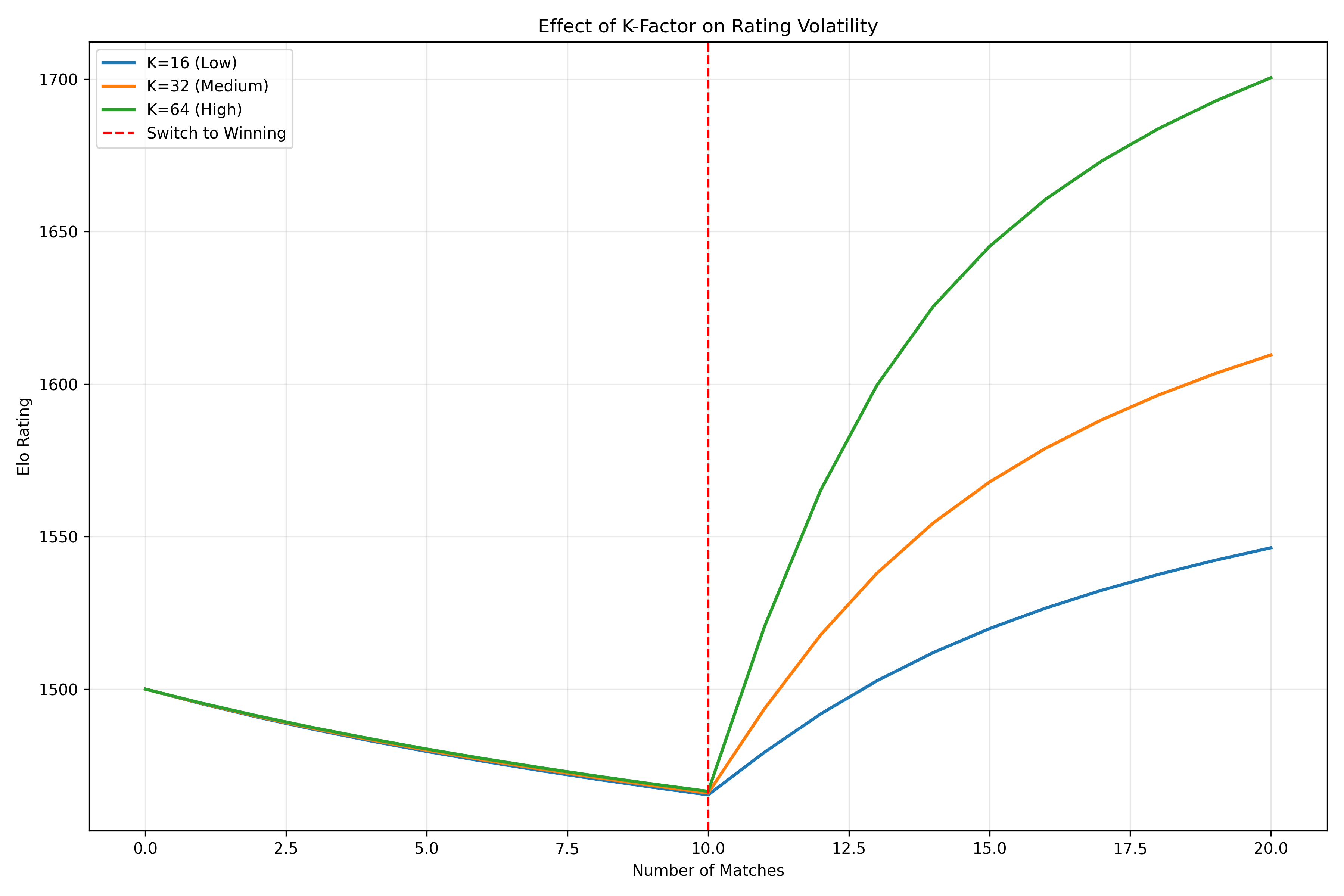
This visualization demonstrates how different K-factors affect rating changes. Higher K-factors lead to more dramatic rating shifts, which is useful for new players whose “true” rating is still being established.

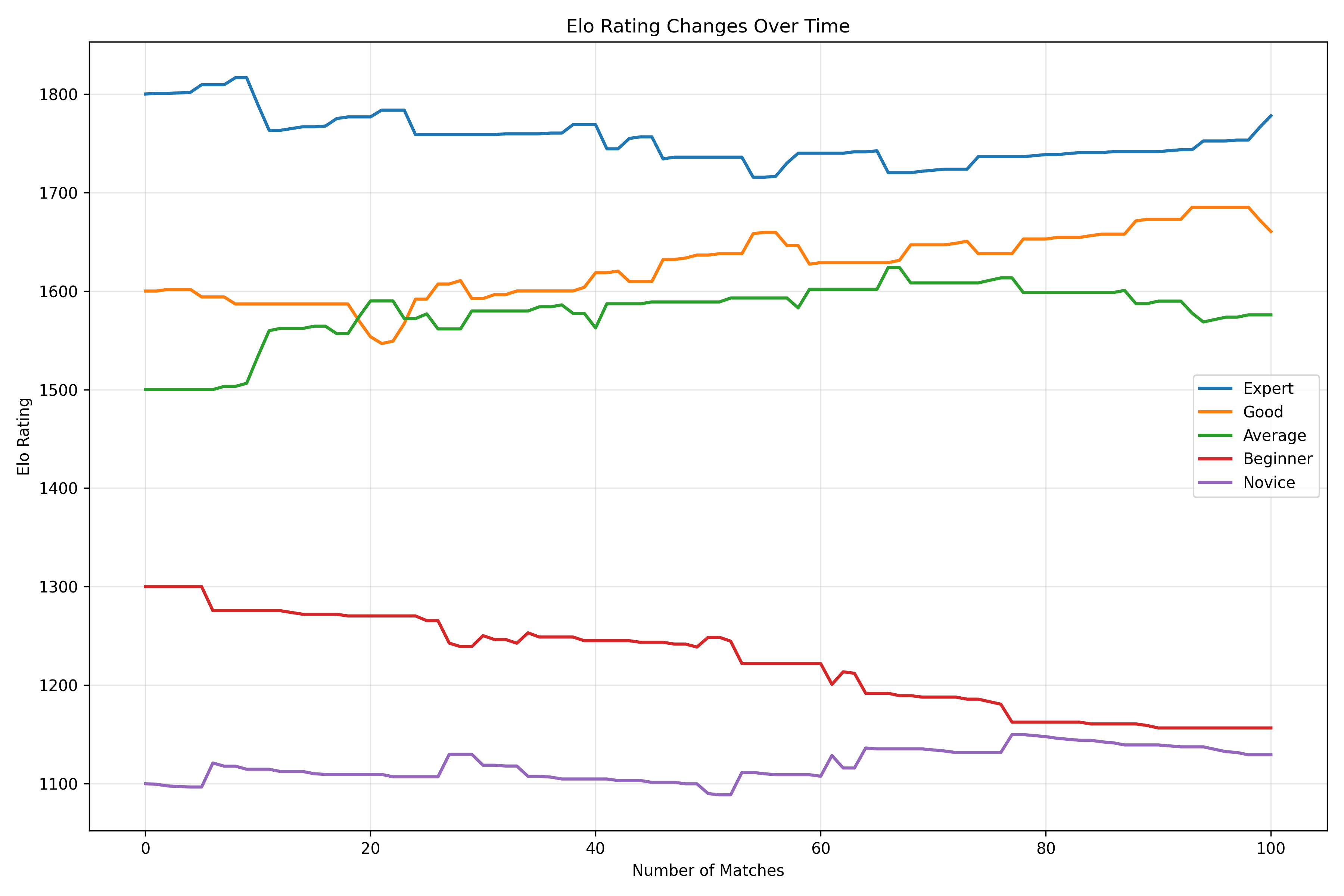
This chart shows how much a player’s rating changes after winning against opponents of different strengths. Notice how beating a much stronger opponent results in a larger rating increase, while beating a much weaker opponent yields minimal gains.

Real-World Example: Ranking Atlanta Taco Spots

Let’s use Elote to solve a real problem - finding the best taco spot in Atlanta:

import random
import matplotlib.pyplot as plt
import numpy as np
import os

# Our contenders
taco_spots = [
    "Taqueria del Sol",
    "Superica",
    "Bartaco",
    "El Rey del Taco",
    "Taqueria La Oaxaqueña",
    "Nuevo Laredo Cantina",
    "Mi Barrio",
    "El Taco Veloz"
]

# Create competitors for each taco spot
competitors = {spot: EloCompetitor(initial_rating=1500) for spot in taco_spots}

# Simulate some taste tests (in real life, you'd use actual comparisons)
def simulate_comparison(a, b):
    # This is just for demonstration - in reality, you'd use real preferences
    weights = {
        "Taqueria del Sol": 7,
        "Superica": 6,
        "Bartaco": 5,
        "El Rey del Taco": 8,
        "Taqueria La Oaxaqueña": 9,
        "Nuevo Laredo Cantina": 6,
        "Mi Barrio": 7,
        "El Taco Veloz": 8
    }
    # Add some randomness to make it interesting
    a_score = weights[a] + random.uniform(-2, 2)
    b_score = weights[b] + random.uniform(-2, 2)
    return a_score > b_score

# Create all possible matchups
matchups = [(a, b) for a in taco_spots for b in taco_spots if a != b]

# Run the tournament
for a, b in matchups:
    if simulate_comparison(a, b):
        competitors[a].beat(competitors[b])
    else:
        competitors[b].beat(competitors[a])

# Display rankings
print("Atlanta Taco Joint Rankings:")
sorted_spots = sorted(competitors.items(), key=lambda x: x[1].rating, reverse=True)
for i, (spot, competitor) in enumerate(sorted_spots):
    print(f"{i+1}. {spot}: {competitor.rating:.1f}")

# Visualize the final ratings
plt.figure(figsize=(10, 6))
spots = [spot for spot, _ in sorted_spots]
ratings = [competitor.rating for _, competitor in sorted_spots]

plt.barh(spots, ratings, color='skyblue')
plt.axvline(x=1500, color='r', linestyle='--', alpha=0.7, label='Initial Rating (1500)')
plt.xlabel('Elo Rating')
plt.title('Atlanta Taco Joint Rankings')
plt.grid(axis='x', alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()

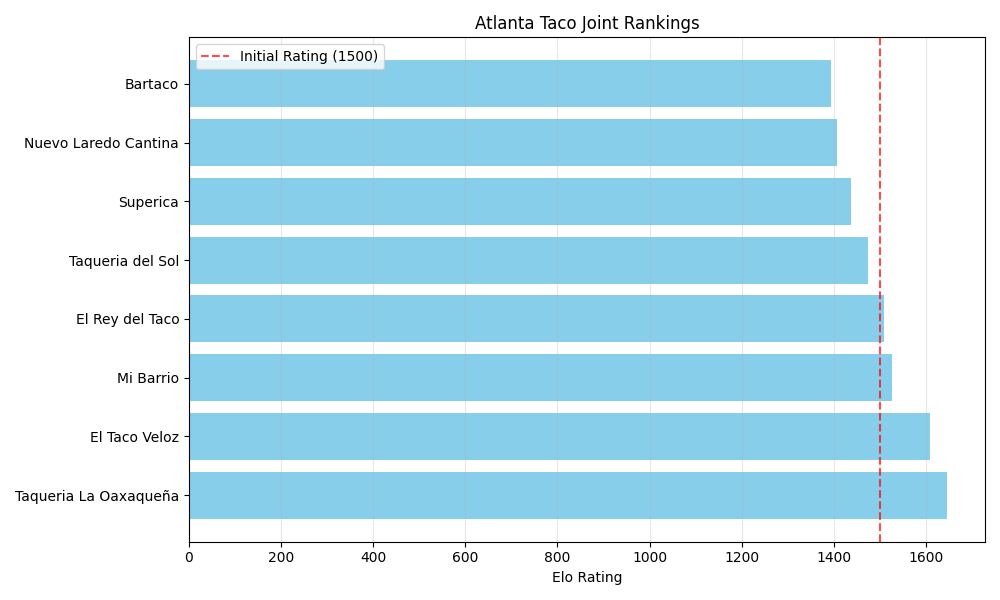
This visualization shows the final Elo ratings of our taco spots after the tournament. Spots with ratings above 1500 performed better than expected, while those below 1500 underperformed.

Pros and Cons of the Elo System

Pros:

• Simple and intuitive: Easy to understand and implement
• Self-correcting: Ratings naturally adjust over time
• Zero-sum: The total rating points in the system remain constant (assuming all matches have the same k, no players join or leave the system, and no minimum rating handling is triggered)
• Predictive: Provides win probabilities for future matchups

Cons:

• Slow to converge: New players need many games to reach their “true” rating
• No uncertainty measure: Doesn’t tell you how confident it is in a rating
• Inflation/deflation: Ratings can drift over time without careful management
• No team dynamics: Doesn’t account for how individuals contribute to team performance
• Assumes transitive performance: If A beats B and B beats C, it assumes A should beat C

When to Use Elo

Elo is best when:

• You need a simple, proven rating system
• You have plenty of comparison data
• The skill being measured is relatively stable
• You’re ranking individuals rather than teams
• You want to provide win probabilities

Conclusion: The Enduring Legacy of Elo

Despite being over 60 years old, the Elo rating system remains remarkably relevant. Its simplicity and effectiveness have made it the foundation for countless ranking systems across sports, games, and even product recommendations.

In the next post in this series, we’ll look at the Glicko rating system, which addresses some of Elo’s limitations by adding a reliability measure to ratings.