Optimal Bankroll Management with Keeks: The Kelly Criterion

In this first post of our series on bankroll management strategies in Keeks, we’ll dive into the Kelly Criterion - the mathematical foundation of optimal betting and the inspiration behind the library’s name.

What is the Kelly Criterion?

The Kelly Criterion is a mathematical formula used to determine the optimal size of a series of bets or investments. Developed by John L. Kelly Jr. at Bell Labs in 1956, it was originally created to solve a problem in information theory but found its true calling in the world of gambling and finance.

At its core, the Kelly Criterion answers a deceptively simple question: “What percentage of your bankroll should you bet to maximize long-term growth?”

The formula is elegantly simple:

f* = (p * b - q) / b

Where:

• f* is the fraction of your bankroll to bet (the Kelly fraction)
• p is the probability of winning
• q is the probability of losing (1 - p)
• b is the net odds received on the bet (payout for a $1 bet)

The Theory Behind Kelly

What makes Kelly special is that it’s mathematically proven to be the optimal strategy for maximizing the logarithm of wealth over the long run. In other words, if your goal is to grow your bankroll as quickly as possible over many bets, Kelly gives you the exact percentage to bet each time.

The Kelly strategy is based on a few key insights:

1. Bet more when you have an edge: The bigger your advantage (higher probability of winning or better odds), the more you should bet.
2. Bet less when you’re uncertain: The formula naturally reduces your bet size when your edge is smaller.
3. Never risk ruin: A pure Kelly strategy will never bet so much that you risk losing your entire bankroll on a single bet.

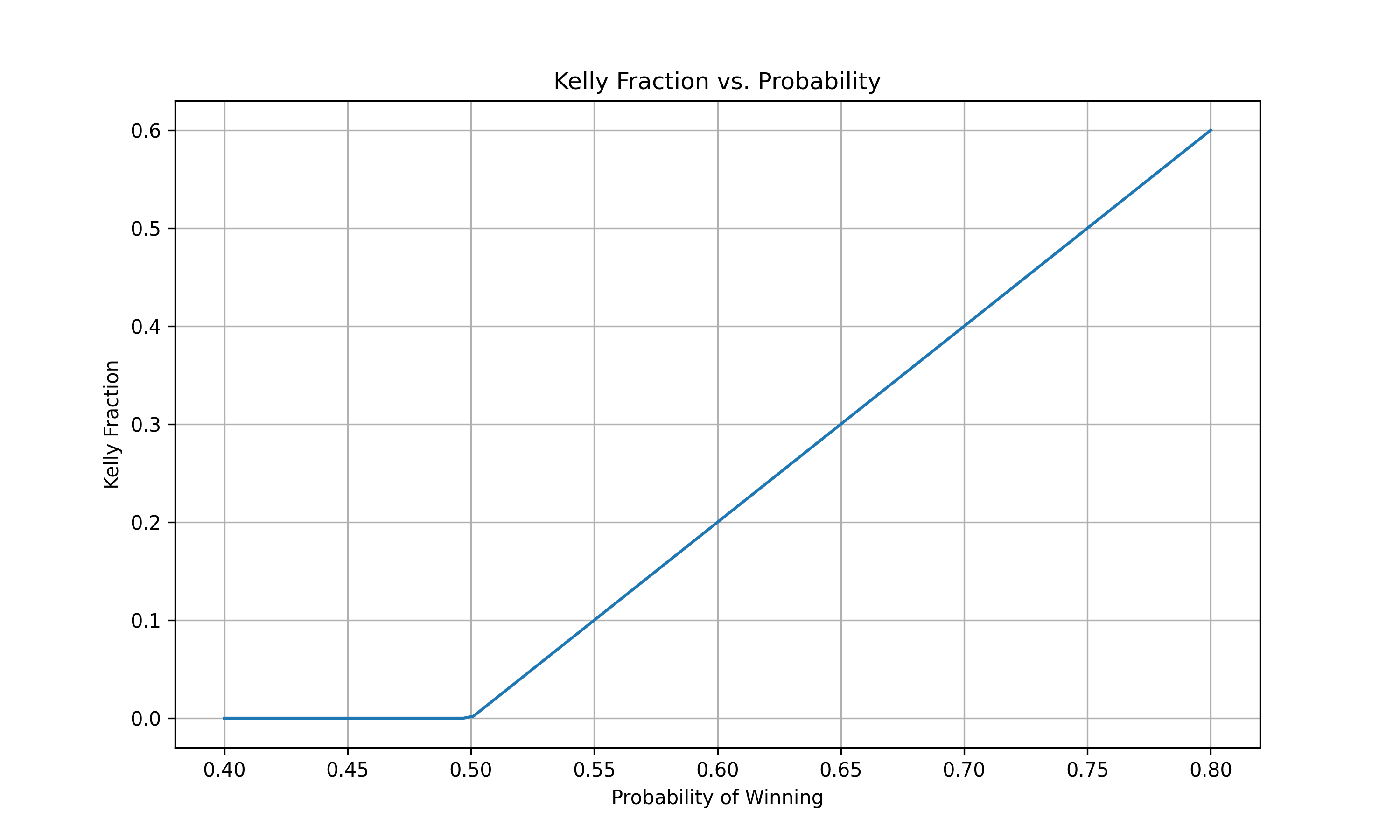
As you can see in the graph above, the Kelly fraction increases as your probability of winning increases. When your probability is below the break-even point (0.5 for even money bets), the Kelly Criterion recommends not betting at all. Here our break-even point is a touch above 0.5 because of transaction costs (not all bets are free).

Pros of the Kelly Criterion

• Mathematically optimal: It’s proven to maximize long-term growth rate.
• Self-adjusting: Automatically bets more when you have a bigger edge.
• Prevents ruin: Properly applied, it ensures you never go broke.
• Compound growth: Leverages the power of compounding returns.

Cons of the Kelly Criterion

• High volatility: Full Kelly betting can lead to significant bankroll swings.
• Requires accurate inputs: The strategy is only as good as your probability estimates.
• Psychologically challenging: The recommended bet sizes can sometimes feel uncomfortably large.
• Not suitable for all situations: In some contexts, maximizing growth rate isn’t the primary goal.

Implementing Kelly in Python

For our implementation, we’ll use Keeks version 0.2.0, an open-source Python library specifically designed for bankroll management and betting strategies. Keeks (named after the Kelly Criterion) provides robust implementations of various betting strategies, bankroll management techniques, and simulation tools.

You can install Keeks using pip:

pip install keeks

For more information, check out the GitHub repository and documentation.

Let’s implement the Kelly Criterion using the Keeks library:

from keeks.bankroll import BankRoll
from keeks.binary_strategies.kelly import KellyCriterion
from keeks.simulators.repeated_binary import RepeatedBinarySimulator

# Create a bankroll with initial funds - using larger amount to avoid ruin
bankroll = BankRoll(initial_funds=10000.0, max_draw_down=0.3)

# Create a Kelly Criterion strategy
# For even odds (1:1) betting, using smaller values:
# loss = 1 (lose $1 if wrong)
# payoff = 1 (gain $1 if right)
# transaction_cost = 0 (no separate fee)
strategy = KellyCriterion(payoff=1.0, loss=1.0, transaction_cost=0.0)

# Create a simulator with a fixed probability
simulator = RepeatedBinarySimulator(
    payoff=1.0,
    loss=1.0,
    transaction_costs=0.0,
    probability=0.6,  # 60% chance of winning
    trials=1000
)

# Run the simulation
simulator.evaluate_strategy(strategy, bankroll)

# Plot the results
bankroll.plot_history()

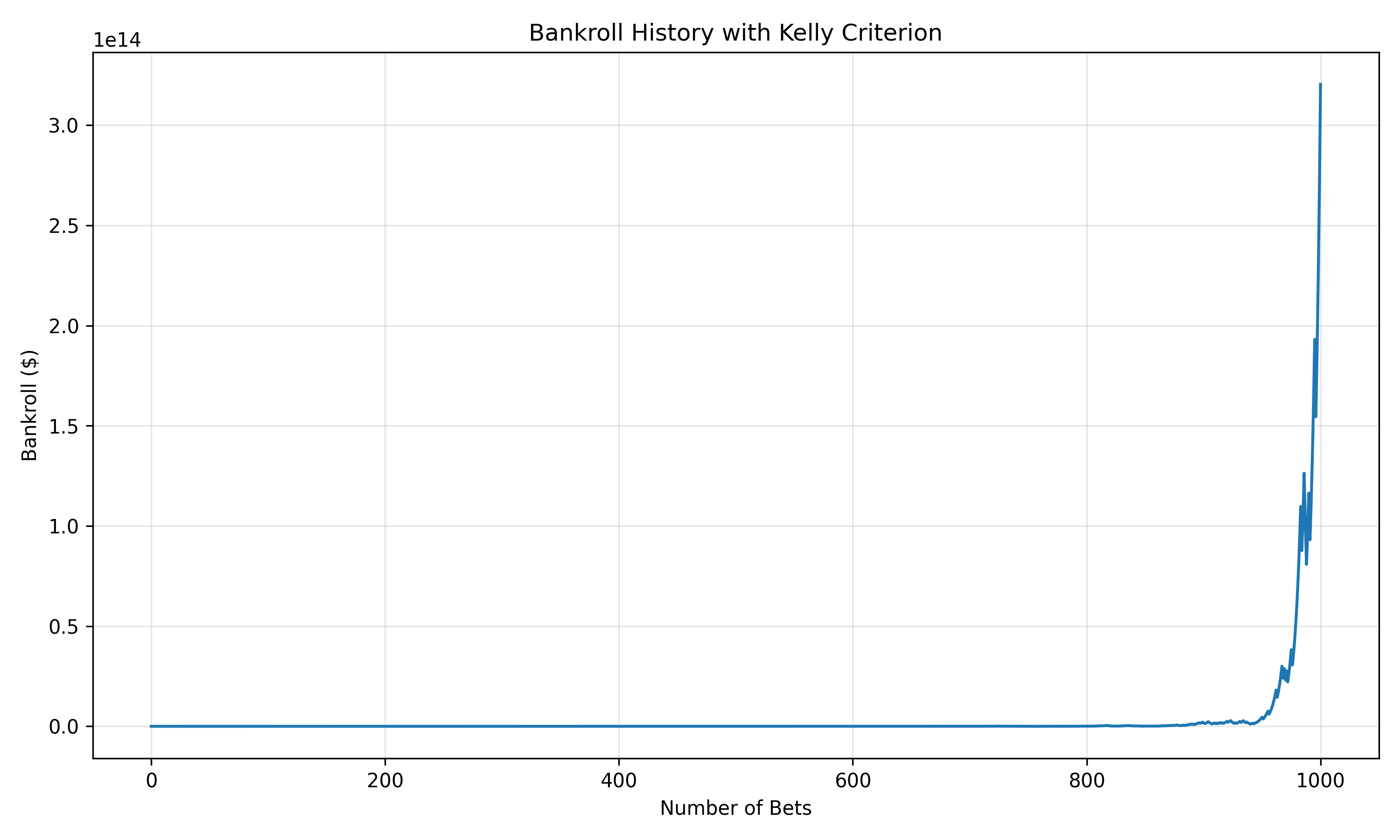
The Keeks library provides a robust implementation of the Kelly Criterion with several advantages:

1. Built-in Bankroll Management: The BankRoll class handles all the bankroll tracking and protection against excessive losses with customizable drawdown limits.
2. Transaction Costs: The library automatically accounts for transaction costs and other fees that impact optimal bet sizing.
3. Simulation Tools: The RepeatedBinarySimulator allows you to test your strategy under controlled conditions with customizable parameters.
4. Visualization: Built-in plotting functions help you visualize your results without writing additional code.
5. Risk Management: Keeks implements safety features that prevent betting too much of your bankroll at once, even when the Kelly Criterion might suggest larger bets.
6. Extensibility: The library is designed to be easily extended with custom strategies beyond just the Kelly Criterion.

Keeks is particularly valuable for anyone looking to implement systematic betting or investment strategies as it handles many of the complexities and edge cases that arise in real-world applications.

Understanding Keeks Parameters for Kelly Criterion

When using the KellyCriterion class in Keeks, it’s important to understand how the parameters work:

• payoff: The amount you gain if you win the bet (not including your original stake)
• loss: The amount you lose if you lose the bet
• transaction_cost: Any additional cost associated with placing the bet

For example, with standard -110 odds in sports betting (bet $110 to win $100):

• Set loss = 1.1 (you lose $1.10 for every $1 bet)
• Set payoff = 1.0 (you gain $1.00 for every $1 bet)
• Set transaction_cost = 0.0 (no additional fees)

These parameters are used to calculate the optimal bet size according to the Kelly formula. In our examples, we’ve scaled down the actual values to avoid ruin (betting too large a portion of your bankroll), but the proportions remain the same.

Kelly Criterion with Varying Edge

The Kelly fraction changes based on your edge (how much better your odds are than the fair odds):

from keeks.binary_strategies.kelly import KellyCriterion
import numpy as np
import matplotlib.pyplot as plt

# Create a range of probabilities
probabilities = np.linspace(0.4, 0.8, 100)
kelly_fractions = []

# Create a mock bankroll value for the evaluate method
mock_bankroll_value = 1000.0

for p in probabilities:
    # For even odds (1:1) betting:
    strategy = KellyCriterion(payoff=1.0, loss=1.0, transaction_cost=0.0)
    # evaluate() already handles negative values appropriately
    kelly_fractions.append(strategy.evaluate(p, mock_bankroll_value))

plt.figure(figsize=(10, 6))
plt.plot(probabilities, kelly_fractions)
plt.title('Kelly Fraction vs. Probability')
plt.xlabel('Probability of Winning')
plt.ylabel('Kelly Fraction')
plt.grid(True)
plt.show()

Note: In Keeks 0.2.0, the evaluate() method requires passing the current bankroll value as a parameter and already handles negative expected values by returning zero (no bet).

Real-World Example: Sports Betting

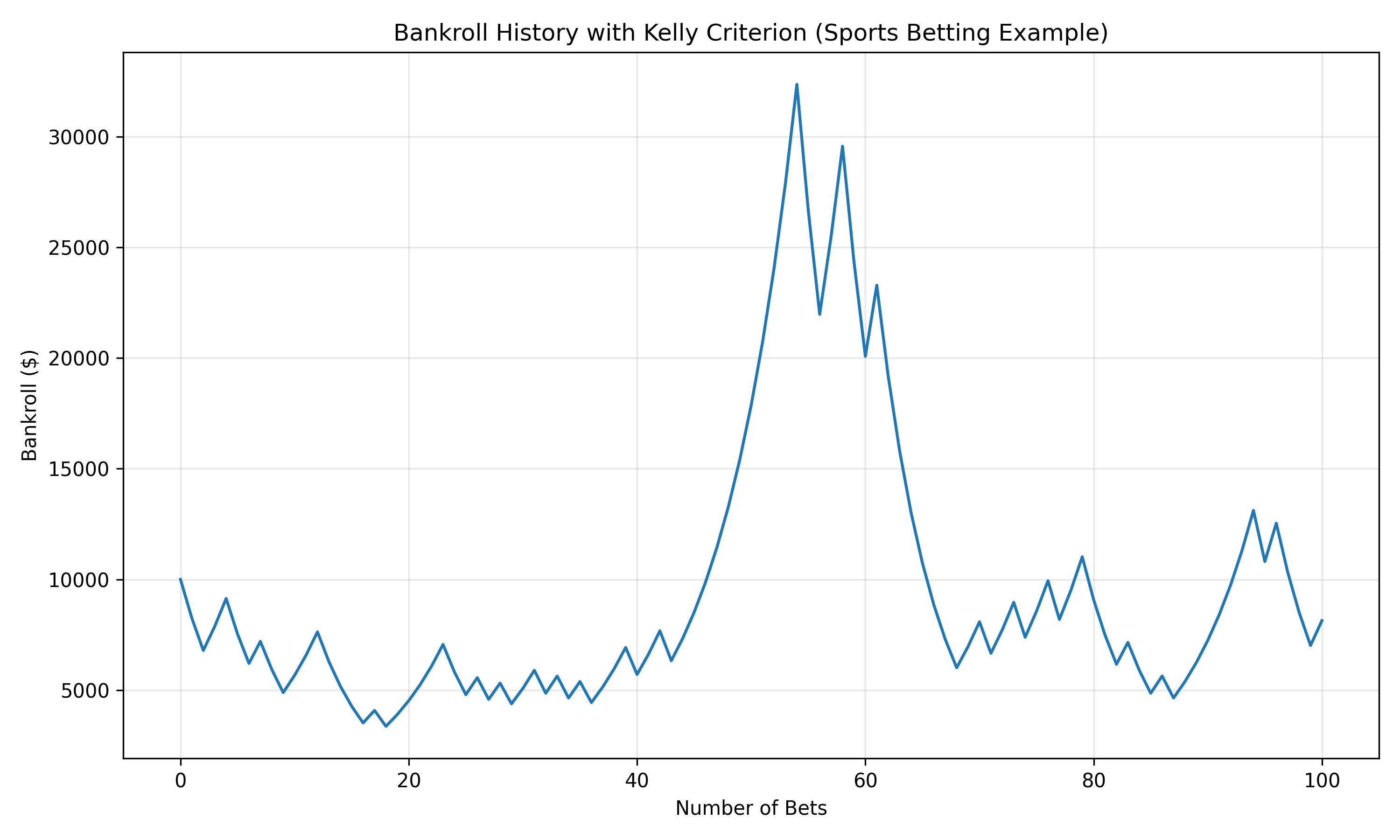
Let’s consider a practical example using Keeks. Suppose you’ve developed a model for NBA games that gives Team A a 60% chance of covering the spread against Team B. The bookmaker is offering standard -110 odds (bet $110 to win $100). In this case you have no edge, so wouldn’t really expect to make a ton of money, but a good bankroll management strategy should keep you from ever losing it all, and ideally should be pretty close to even.

from keeks.bankroll import BankRoll
from keeks.binary_strategies.kelly import KellyCriterion

# Define parameters
win_probability = 0.60  # Your model's estimate
# Standard -110 odds: bet $110 to win $100, but scaling down values
# Using loss/gain approach:
loss = 1.1           # Lose $1.10 if wrong
payoff = 1.0         # Gain $1.00 if right
transaction_cost = 0.0 # No separate transaction fee
bankroll_amount = 10000.0  # Larger bankroll to avoid ruin

# Create a bankroll instance
bankroll = BankRoll(initial_funds=bankroll_amount, max_draw_down=0.3)

# Create Kelly strategy
strategy = KellyCriterion(
    payoff=payoff,
    loss=loss,
    transaction_cost=transaction_cost
)

# Calculate optimal bet size
kelly_fraction = strategy.evaluate(win_probability, bankroll.total_funds)
bet_amount = kelly_fraction * bankroll.bettable_funds

print(f"Kelly fraction: {kelly_fraction:.4f}")
print(f"Recommended bet: ${bet_amount:.2f}")

When to Use Kelly

The Kelly Criterion is most appropriate when:

1. You have a good estimate of the true probability of winning
2. You’re making many bets over time
3. Your goal is to maximize long-term growth
4. You can tolerate significant short-term volatility

Many professional gamblers and investors use a “Fractional Kelly” approach (which we’ll cover in the next post) to reduce volatility while still capturing most of the growth benefits.

Conclusion

The Kelly Criterion represents the mathematical pinnacle of bankroll management - a strategy that, with perfect information, cannot be beaten for long-term growth. While its practical application requires careful consideration of your risk tolerance and the accuracy of your probability estimates, understanding Kelly is fundamental to any serious discussion of optimal betting.

In the next post, we’ll explore the Fractional Kelly approach, which addresses some of the volatility concerns while preserving much of the growth potential.