Glicko-2: Adding Volatility to the Rating Equation

In our previous posts, we explored Elo Rating System and Glicko-1 Rating System. Glicko-1 improved on Elo by tracking rating reliability, but it still missed something important: some players are just more consistent than others.

Enter Glicko-2, which adds a third dimension to the rating equation: volatility.

The Evolution Continues: From Reliability to Volatility

Mark Glickman wasn’t done innovating after Glicko-1. In 2001, he published the Glicko-2 system, which added a volatility parameter to track how consistently a player performs.

Think about it: some players deliver the same level of performance day in and day out. Others are wildly inconsistent - brilliant one day, terrible the next. In Glicko-1, both types of players might have the same rating and RD, but they’re fundamentally different in terms of predictability.

Glickman’s insight was to add a volatility parameter (σ) that measures how much a player’s underlying skill tends to fluctuate over time. A player with low volatility has stable performance, while a player with high volatility has unpredictable swings in performance.

How Glicko-2 Works: The Three-Dimensional Rating

Glicko-2 tracks three values for each player:

1. Rating (r): Skill level (same as Elo and Glicko-1)
2. Rating Deviation (RD): Uncertainty in the rating (same as Glicko-1)
3. Volatility (σ): How much the player’s true skill tends to fluctuate

The system also introduces a few other refinements:

• Ratings are calculated on an internal scale and then converted to the Glicko scale
• The update algorithm uses an iterative approach to find the new volatility
• Rating periods are more explicitly defined than in Glicko-1. Elote v1.1.0+ uses the match_time parameter provided with each match to calculate RD increases and volatility updates based on actual time elapsed, leading to more precise modeling.

The mathematical details are quite complex (involving partial derivatives and iterative optimization), but the core idea is that a player’s new rating depends not just on match outcomes and rating reliability, but also on how consistent their performance has been historically.

Implementing Glicko-2 with Elote

Let’s see how this works in practice with Elote:

from elote import Glicko2Competitor
import datetime

# Create two competitors with different volatilities
steady_player = Glicko2Competitor(initial_rating=1500, initial_rd=50, initial_volatility=0.3)
erratic_player = Glicko2Competitor(initial_rating=1500, initial_rd=50, initial_volatility=0.9)

# Check win probability
print(f"Win probability: {steady_player.expected_score(erratic_player):.4%}")

# Let's simulate a series of matches with mixed results
base_time = datetime.datetime.now()
for i in range(5):
    match_timestamp = base_time + datetime.timedelta(days=i)
    steady_player.beat(erratic_player, match_time=match_timestamp)
    
for i in range(5):
    match_timestamp = base_time + datetime.timedelta(days=i+5)
    erratic_player.beat(steady_player, match_time=match_timestamp)

# See how ratings, RDs, and volatilities changed
print(f"Steady player: Rating={steady_player.rating:.1f}, RD={steady_player.rd:.1f}, Vol={steady_player.volatility:.3f}")
print(f"Erratic player: Rating={erratic_player.rating:.1f}, RD={erratic_player.rd:.1f}, Vol={erratic_player.volatility:.3f}")

Notice how the erratic player’s volatility remains higher after the mixed results, while the steady player’s volatility decreases despite the same win-loss record.

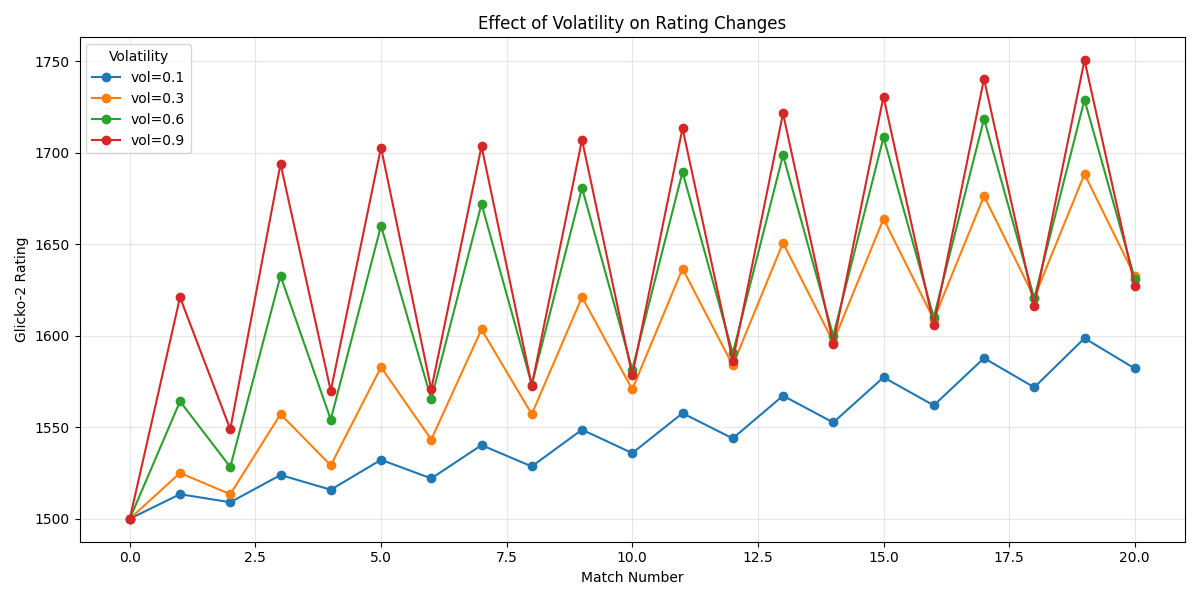
The graph above shows how players with different volatility values respond to the same pattern of wins and losses. Players with higher volatility (like the orange line) experience more dramatic rating changes compared to players with lower volatility (like the blue line).

Real-World Example: Ranking NBA Players

Let’s use Glicko-2 to rank NBA players, accounting for both reliability and consistency:

from elote import Glicko2Competitor
import random
import datetime

# Some top NBA players
nba_players = [
    "LeBron James",
    "Kevin Durant",
    "Stephen Curry",
    "Giannis Antetokounmpo",
    "Nikola Jokić",
    "Luka Dončić",
    "Joel Embiid",
    "Kawhi Leonard",
    "Damian Lillard",
    "Jayson Tatum"
]

# Base skill levels (just for demonstration)
base_skills = {
    "LeBron James": 95,
    "Kevin Durant": 94,
    "Stephen Curry": 93,
    "Giannis Antetokounmpo": 94,
    "Nikola Jokić": 95,
    "Luka Dončić": 92,
    "Joel Embiid": 93,
    "Kawhi Leonard": 92,
    "Damian Lillard": 90,
    "Jayson Tatum": 91
}

# Consistency factors (lower means more consistent)
consistency = {
    "LeBron James": 3,  # Very consistent
    "Kevin Durant": 4,
    "Stephen Curry": 6,  # Can have off nights from 3
    "Giannis Antetokounmpo": 4,
    "Nikola Jokić": 3,  # Very consistent
    "Luka Dončić": 5,
    "Joel Embiid": 7,  # Injury-prone, inconsistent
    "Kawhi Leonard": 8,  # Load management affects consistency
    "Damian Lillard": 5,
    "Jayson Tatum": 6
}

# Simulate player matchups with varying consistency
def simulate_comparison(a, b):
    # Simulate performance with appropriate variance
    a_performance = base_skills[a] + random.uniform(-consistency[a], consistency[a])
    b_performance = base_skills[b] + random.uniform(-consistency[b], consistency[b])
    
    return a_performance > b_performance

# Create matchups
matchups = []
for _ in range(100):  # 100 random matchups
    a = random.choice(nba_players)
    b = random.choice([p for p in nba_players if p != a])
    matchups.append((a, b))

# Create competitors for each player
competitors = {player: Glicko2Competitor(initial_rating=1500, initial_rd=350, initial_volatility=0.06) for player in nba_players}

# Simulate the tournament manually
base_time = datetime.datetime.now()
for i, (a, b) in enumerate(matchups):
    match_timestamp = base_time + datetime.timedelta(minutes=i)
    if simulate_comparison(a, b):
        competitors[a].beat(competitors[b], match_time=match_timestamp)
    else:
        competitors[b].beat(competitors[a], match_time=match_timestamp)

# Display rankings with all three parameters
print("NBA Player Rankings:")
for i, (player, rating) in enumerate(sorted([(p, competitors[p].rating) for p in nba_players], key=lambda x: x[1], reverse=True)):
    rd = competitors[player].rd
    vol = competitors[player].volatility
    print(f"{i+1}. {player}: {rating:.1f} ± {rd:.1f} (Vol: {vol:.3f})")

This example shows how Glicko-2 can capture not just skill level and rating confidence, but also performance consistency.

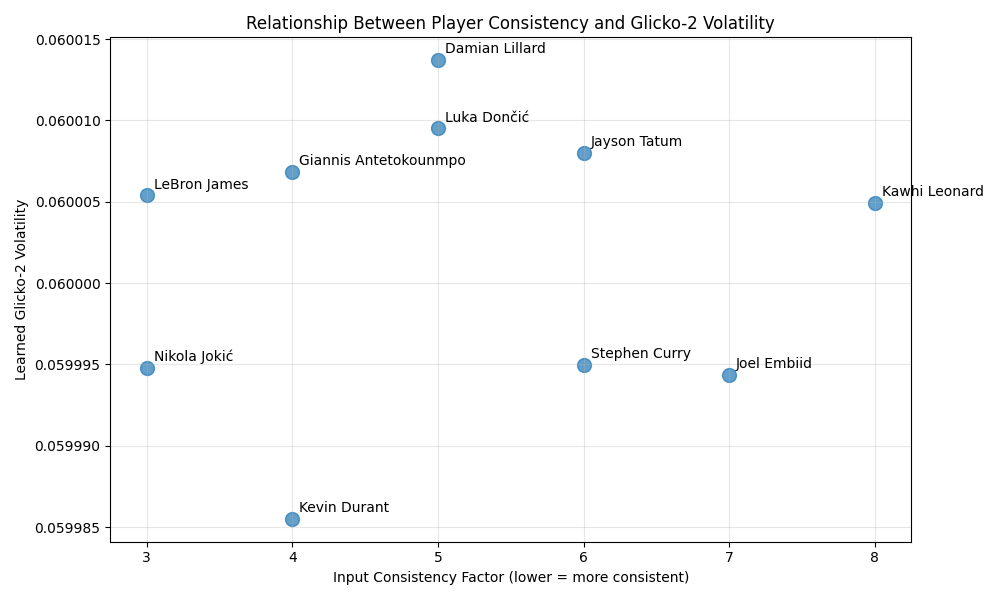
The scatter plot above shows the relationship between the input consistency factors (lower means more consistent) and the learned Glicko-2 volatility values. Players who are more consistent in their performances (like LeBron James and Nikola Jokić) tend to have lower volatility values, while players with more variable performances (like Kawhi Leonard) develop higher volatility values.

Pros and Cons of the Glicko-2 System

Pros:

• Tracks volatility: Distinguishes between consistent and inconsistent performers
• More accurate predictions: Accounts for more factors than Elo or Glicko-1
• Handles inactivity well: Uncertainty increases appropriately during inactive periods
• Converges quickly: Ratings stabilize faster than with Elo or Glicko-1
• Theoretically sound: Based on solid statistical principles

Cons:

• Complexity: Significantly more complex than Elo or Glicko-1
• Computational cost: More expensive to calculate, especially the volatility update
• Parameter tuning: Requires careful selection of system parameters
• Less intuitive: Harder to explain to non-technical users
• Overkill for simple use cases: May be unnecessarily complex for basic applications

When to Use Glicko-2

Glicko-2 is best when:

• You need the most accurate ratings possible
• Performance consistency is an important factor
• You have sufficient data to estimate volatility reliably
• Computational complexity isn’t a concern
• You’re dealing with a competitive system where small rating advantages matter

Conclusion: The Power of Tracking Consistency

Glicko-2 represents the pinnacle of the Glicko family of rating systems. By tracking not just skill and uncertainty but also consistency, it provides a three-dimensional view of competitor performance that can lead to more accurate ratings and predictions.

Is it overkill for ranking your favorite pizza places? Probably. But for serious competitive systems where accuracy matters - from chess tournaments to matchmaking in competitive games - Glicko-2 offers advantages that can make the additional complexity worthwhile.

In our next post, we’ll shift gears and explore the TrueSkill rating system, which was developed by Microsoft for Xbox Live and takes yet another approach to the rating problem.

Until then, may your ratings be high, your deviations low, and your volatility just right!