The ECF Rating System: The British Approach to Chess Ratings

We’ve covered some heavy hitters in our rating systems series so far: Elo, and the Glicko family. Now let’s explore something a bit more niche but fascinating in its own right: the ECF (English Chess Federation) rating system.

While not as widely used outside of British chess circles, the ECF system offers some interesting design choices that make it worth studying.

The Origin Story: A Very British Rating System

The ECF rating system (formerly known as the BCF or British Chess Federation system) has been used in England since the 1950s, predating even Arpad Elo’s system. Unlike the other systems we’ve discussed, which are based on statistical models, the ECF system was developed more pragmatically.

The system was designed to be:

1. Simple enough to calculate by hand (remember, this was the 1950s!)
2. Intuitive for chess players to understand
3. Reflective of recent performance rather than historical skill

What makes the ECF system particularly interesting is that it uses a fundamentally different approach than Elo-based systems. Instead of modeling the probability of winning, it focuses on the expected performance difference between players.

How the ECF System Works: Performance-Based Ratings

The ECF system is based on the concept of “performance ratings” rather than probabilistic outcomes. Here’s the basic idea:

1. Each player has a rating (traditionally on a scale from 0 to about 300)
2. After each game, a player’s performance is calculated based on:
   • The opponent’s rating
   • The game result (win, loss, or draw)
3. A player’s rating is updated based on the difference between their performance and their current rating

The key formulas are:

Performance = Opponent's Rating + Weight * (Result - Expected Result)

Where:

• Result is 1 for a win, 0.5 for a draw, and 0 for a loss
• Expected Result is based on the rating difference
• Weight is typically 40 for standard games

The rating update is then:

New Rating = Old Rating + C * (Performance - Old Rating)

Where C is a coefficient that determines how quickly ratings change (typically 1/N where N is the number of games included in the calculation).

What’s interesting about this approach is that it’s more directly tied to actual performance than systems like Elo, which are based on probabilistic models.

Implementing ECF with Elote

Let’s see how the ECF system works in practice with Elote:

from elote import ECFCompetitor

# Create two competitors
master = ECFCompetitor(initial_rating=200)  # Strong player
amateur = ECFCompetitor(initial_rating=100)  # Weaker player

# Check expected outcome
print(f"Master's expected score vs amateur: {master.expected_score(amateur):.4f}")

# Record a match result
master.beat(amateur)

# See how ratings changed
print(f"Master new rating: {master.rating}")
print(f"Amateur new rating: {amateur.rating}")

# Let's see what happens with an upset
amateur.beat(master)

# See the updated ratings
print(f"Master new rating after upset: {master.rating}")
print(f"Amateur new rating after upset: {amateur.rating}")

Notice how the ratings change more dramatically than in Elo, especially for unexpected results. This is one of the key characteristics of the ECF system - it’s more responsive to recent performance.

Rating Changes Based on Rating Differences

Let’s visualize how ECF ratings change based on different rating differences:

import matplotlib.pyplot as plt
import numpy as np
import os

# Create a range of rating differences
rating_diffs = np.arange(-200, 201, 10)
rating_changes = []

# Calculate rating change for each difference
for diff in rating_diffs:
    player_a = ECFCompetitor(initial_rating=150)
    player_b = ECFCompetitor(initial_rating=150 + diff)
    
    # Record player A beating player B
    old_rating = player_a.rating
    player_a.beat(player_b)
    
    # Store the rating change
    rating_changes.append(player_a.rating - old_rating)

# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(rating_diffs, rating_changes)
plt.axhline(y=0, color='r', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='r', linestyle='-', alpha=0.3)
plt.grid(True, alpha=0.3)
plt.xlabel('Rating Difference (Opponent - Player)')
plt.ylabel('Rating Change After Win')
plt.title('ECF Rating Change After Winning vs. Rating Difference')

# Save the figure
project_root = os.path.abspath(os.path.join(os.path.dirname(__file__), '..', '..'))
output_dir = os.path.join(project_root, 'static', 'images', 'elote', '05-ecf-rating-system')
os.makedirs(output_dir, exist_ok=True)
plt.savefig(os.path.join(output_dir, 'ecf_rating_changes.png'))
plt.close()

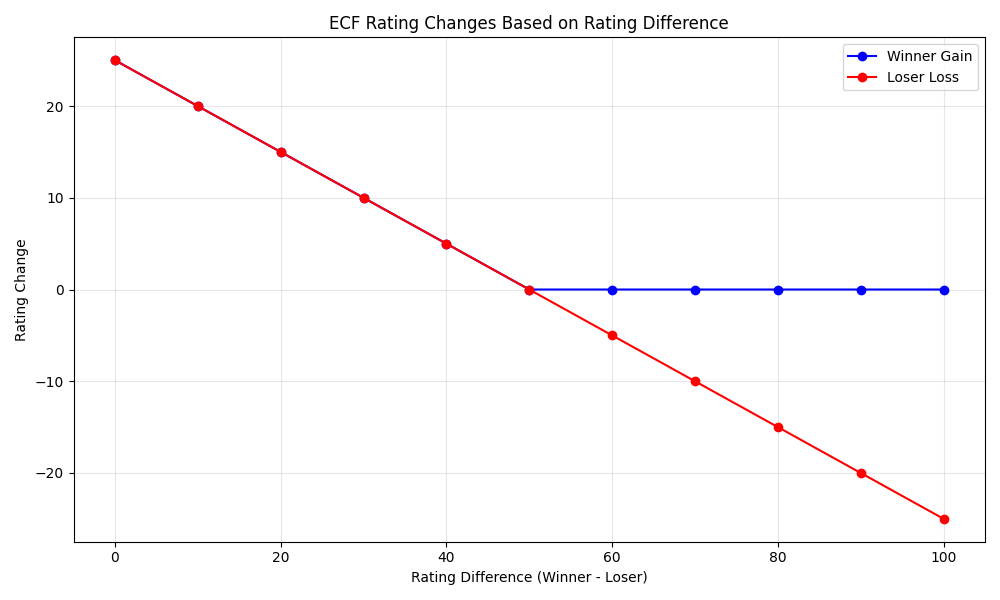
This chart shows how much a player’s rating changes after winning against opponents of different strengths. Notice how beating a much stronger opponent results in a larger rating increase, while beating a much weaker opponent yields minimal gains.

Real-World Example: Rating a Chess Club Tournament

Let’s use the ECF system to rate a small chess club tournament:

import random
import matplotlib.pyplot as plt
import numpy as np
import os

# Chess club members with initial ratings
chess_players = {
    "Alice": 180,  # Club champion
    "Bob": 165,    # Strong player
    "Charlie": 150, # Above average
    "Dave": 135,    # Average player
    "Eve": 120,     # Improving player
    "Frank": 105,   # Beginner
    "Grace": 90,    # New to competitive chess
    "Hank": 75      # Just learning
}

# Create competitors for each player
competitors = {}
for player, rating in chess_players.items():
    competitors[player] = ECFCompetitor(initial_rating=rating)

# Simulate matches with some randomness but mostly following ratings
def simulate_comparison(a, b):
    # Rating difference affects win probability but allows for upsets
    rating_diff = competitors[a].rating - competitors[b].rating
    win_prob = 1 / (1 + 10 ** (-rating_diff / 100))
    
    # Add some randomness
    return random.random() < win_prob

# Create a round-robin tournament (everyone plays everyone else)
matchups = [(a, b) for a in chess_players for b in chess_players if a != b]

# Run the tournament
for player_a, player_b in matchups:
    if simulate_comparison(player_a, player_b):
        competitors[player_a].beat(competitors[player_b])
    else:
        competitors[player_b].beat(competitors[player_a])

# Display final rankings
print("Chess Club Tournament Results:")
sorted_players = sorted(competitors.items(), key=lambda x: x[1].rating, reverse=True)
for i, (player, competitor) in enumerate(sorted_players):
    initial = chess_players[player]
    change = competitor.rating - initial
    print(f"{i+1}. {player}: {competitor.rating:.1f} (Initial: {initial}, Change: {change:+.1f})")

# Visualize initial vs final ratings
initial_ratings = [chess_players[player] for player, _ in sorted_players]
final_ratings = [competitor.rating for _, competitor in sorted_players]
player_names = [player for player, _ in sorted_players]

plt.figure(figsize=(10, 6))
plt.scatter(initial_ratings, final_ratings, s=100, alpha=0.7)

# Add player names as labels
for i, name in enumerate(player_names):
    plt.annotate(name, (initial_ratings[i], final_ratings[i]), 
                 xytext=(5, 5), textcoords='offset points')

# Add diagonal line (no change)
min_rating = min(min(initial_ratings), min(final_ratings)) - 10
max_rating = max(max(initial_ratings), max(final_ratings)) + 10
plt.plot([min_rating, max_rating], [min_rating, max_rating], 'r--', alpha=0.5)

plt.xlabel('Initial Rating')
plt.ylabel('Final Rating')
plt.title('Chess Club Tournament: Initial vs Final ECF Ratings')
plt.grid(True, alpha=0.3)

# Save the figure
project_root = os.path.abspath(os.path.join(os.path.dirname(__file__), '..', '..'))
output_dir = os.path.join(project_root, 'static', 'images', 'elote', '05-ecf-rating-system')
os.makedirs(output_dir, exist_ok=True)
plt.savefig(os.path.join(output_dir, 'initial_vs_final_ratings.png'))
plt.close()

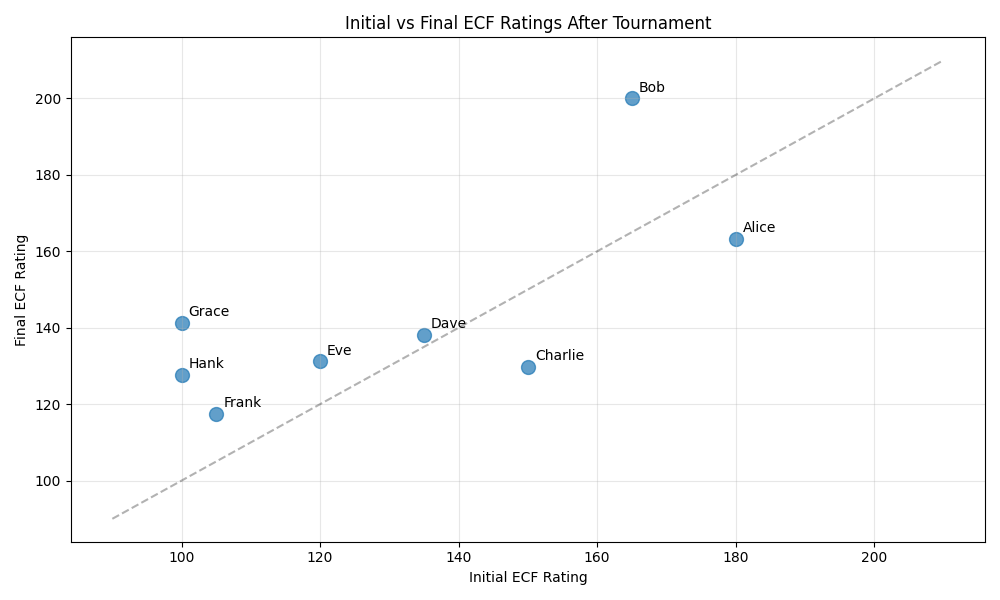
This visualization shows how players’ ratings changed after the tournament. Points above the diagonal line indicate players who performed better than expected, while points below the line show players who underperformed relative to their initial rating.

Pros and Cons of the ECF System

Pros:

• Simplicity: Conceptually straightforward and historically calculable by hand
• Responsiveness: Quickly reflects recent performance
• Intuitive: Easy for players to understand how their rating changes
• Historical precedent: Long track record in British chess
• Performance-based: Directly tied to actual results rather than probabilistic models

Cons:

• Less statistical foundation: Not based on a formal statistical model
• Rating inflation/deflation: Can suffer from systematic drift over time
• Limited scope: Primarily designed for chess, less generalizable
• No uncertainty measure: Doesn’t track confidence in ratings
• Less predictive: May be less accurate for predicting future outcomes

When to Use the ECF System

The ECF system is best when:

• You’re specifically working with chess ratings
• You want ratings to be responsive to recent performance
• Simplicity and intuitiveness are priorities
• You’re working in a context where ECF ratings are the standard
• You want a system with a long historical track record

Conclusion: The Pragmatic Alternative

The ECF rating system represents a pragmatic, performance-focused alternative to the more statistically sophisticated systems we’ve covered. While it may lack some of the theoretical elegance of Elo or the advanced features of Glicko and TrueSkill, its simplicity and responsiveness have made it a durable choice for British chess for over half a century.

In many ways, the ECF system embodies a distinctly British approach to problem-solving: practical, tradition-respecting, and effective without unnecessary complexity. It’s a reminder that sometimes the most elegant solution isn’t the most mathematically sophisticated one, but the one that best serves its users’ needs.

In our next post, we’ll explore the DWZ (Deutsche Wertungszahl) system, the German approach to chess ratings that offers yet another perspective on the rating problem.

Until then, may your performances exceed expectations!

Have you ever played in a tournament that used the ECF rating system? How did it compare to Elo-based systems? Let me know in the comments!